Gyroelongated square bicupola
| Gyroelongated square bicupola | |
|---|---|
 | |
| Type | Johnson J44 – J45 – J46 |
| Faces | 24 triangles 10 squares |
| Edges | 56 |
| Vertices | 24 |
| Vertex configuration | |
| Symmetry group | |
| Properties | convex, chiral |
| Net | |
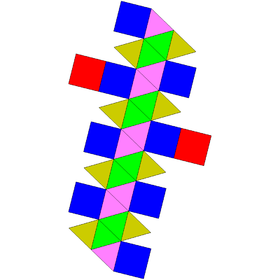 | |
In geometry, the gyroelongated square bicupola is the Johnson solid constructed by attaching two square cupolae on each base of octagonal antiprism. It has the property of chirality.
Construction
[edit]The gyroelongated square bicupola is constructed by attaching two square cupolae on each base of octagonal antiprism, a process known as gyroelongation. This construction involves the removal of octagons, and replacing them with cupolae.[1] As a result, this polyhedron has twenty triangular and ten square faces.[2] The Johnson solid is the convex polyhedron with all of its faces are regular, and the gyroelongated square bicupola is one of them, enumerated as .[3]
Properties
[edit]Given that the edge length , the surface area is: the total area of twenty equilateral triangles and ten squares. Its volume is: the total volume of two square cupolae and an octagonal antiprism.[2] Its dihedral angles can be calculated by adding the components of cupolae and antiprism. The dihedral angle of antiprism between two adjacent triangles is approximately . The dihedral angle of each cupola between two squares is , and that between triangle and square is . The dihedral angle of the cupolae and antiprism between two adjacent triangles and triangle-square is and , respectively.[4]
The gyroelongated square bicupola is one of five Johnson solids, which is chiral, meaning that they have a "left-handed" and a "right-handed" form. In the following illustration, each square face on the left half of the figure is connected by a path of two triangular faces to a square face below it and on the left. In the figure of opposite chirality (the mirror image of the illustrated figure), each square on the left would be connected to a square face above it and on the right. These two chiral forms are not considered different Johnson solids.[citation needed] It has the symmetry of dihedral group .[4]
References
[edit]- ^ Rajwade, A. R. (2001). Convex Polyhedra with Regularity Conditions and Hilbert's Third Problem. Texts and Readings in Mathematics. Hindustan Book Agency. p. 84–89. doi:10.1007/978-93-86279-06-4. ISBN 978-93-86279-06-4.
- ^ a b Berman, Martin (1971). "Regular-faced convex polyhedra". Journal of the Franklin Institute. 291 (5): 329–352. doi:10.1016/0016-0032(71)90071-8. MR 0290245.
- ^ Francis, Darryl (2013). "Johnson solids & their acronyms". Word Ways. 46 (3): 177.
- ^ a b Johnson, Norman W. (1966). "Convex polyhedra with regular faces". Canadian Journal of Mathematics. 18: 169–200. doi:10.4153/CJM-1966-021-8. MR 0185507. S2CID 122006114.











